
(This may seem trivial due to how powerful computers are today but a large amount of that power comes from designing them to be very efficient.)Īnd finally, what about arithmetic? Unfortunately with this method of representing positive and negative numbers it is not practical to perform arithmetic operations on them. For computers having to interpret it the processing required increases. For humans reading it it becomes much easier to make mistakes. There is actually no reason we couldn't do this however it has 2 undesirable effects.

Or put the sign bit as the right most bit. Use only the required number of bits and make the last bit only the sign bit. One might ask why that has to be the case.

We mentioned above that the left most bit is usually the one designated to be the one that indicates the sign of the number and that because of this we need to specify how many bits will be used and that every number must be padded out to that number of bits. For a total of 255 possible numbers represented.01111111 - representing 127, the largest possible number.11111111 - representing -127, the smallest number possible.For a total of 256 possible numbers represented.11111111 - representing 255, the largest number possible.00000000 - representing 0, the smallest number possible.With unsigned (or no negative numbers) with 8 bits we have: In fact, with sign magnitude we actually have just under half because zero may be represented as either 1000000 or 00000000. This is because there are still the same number of combinations of 1's and 0's but now half of them are given to representing negative numbers. The largest number we may represent (With a given number of bits is effectively halved. Representing negative numbers in binary has some interesting side effects.
#NEGATIVE DECIMAL TO BINARY CONVERTER ONLINE 64 BITS#
You could just as easily have used 16, 32, 64 bits etc. In the example above we have numbers being represented using 8 bits. Because we have to designate a specific bit to be the sign indicator, we have to specify how many bits the numbers will be represented using, and pad out accordingly. The above example illustrates an important point when dealing with negative numbers in binary. Usually a '0' indicates the number is positive and a '1' indicates the number is negative. With sign magnitude we designate one of the bits (usually the far left, also known as the most significant bit) to indicate whether a number is positive or negative. Understanding sign magnitude will help you better understand and appreciate the other methods however so I would recommend you don't skip this section. It is not used very often though as it is also the least practical (which you'll soon see). Sign magnitude (sometimes also referred to as sign modulus) is the easiest of the methods we may use. We'll first investigate two early implementations of representing negative numbers, along with their shortcomings, before going into detail with 2's Complement which is the method used most commonly. In binray we don't have this luxury as we are limited to only 1's and 0's.
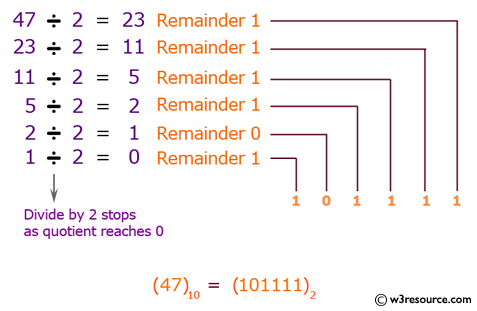
In normal decimal numbers we may simply place a negative sign ( - ) in front of the number to indicate that it is negative. There are a few ways to represent negative numbers in binary. Up until now things have been reasonably straight forward. Table of the First hundred Binary numbers in Decimalįor your convenience, the following table shows the binary numbers from 0 to 1100100 along with their Decimal representation.The complement to positive numbers. Practice a few times, and you’ll be speaking the language of computers with ease. If you want to try it out for yourself, you can use the binary to decimal calculator on this page to check your work. Everything else is indicated by a zero, so we don’t need to include them! 11001100 in binary is the decimal 204. In this case, we need to add 128, 64, 8, and 4 to find the decimal. Remember, we only “use” them when they correspond to a one. All we need to do is add the powers of 2 we used.


 0 kommentar(er)
0 kommentar(er)
